速さと比
同じ距離を進む

「速さと比」なのですが、特に重要となる2つのケースがあります。
・2人の進む時間が同じとき
・2人の進む距離が同じとき
ここからは、「2人の進む距離が同じとき」について見ていきます。
速さの主役と言ってもよいテーマです。
登場する2人が、同じ距離を進むケース
距離の比が1:1のとき
例
速さ × 時間 = 距離
3 × 5 = ①
5 × 3 = ①

2人の進む距離が同じとき、上の式のように、(速さの比)と(時間の比)が逆になります。
逆比と呼ばれます。
逆比は、比を学習したときにしっかりやりましたね。
このように、「登場する2人が同じ距離を進むケース」なのですが、中学受験算数における最頻出問題となっています。
旅人算的解法が全く通用しないため、多くの子どもたちが苦手とする問題です。
また、線分図での状況整理がやりにくいことも、多くの子どもたちが苦手とする一因です。
何はともあれ、このケースの出題は非常に多いのです。
最重要の「型」として、しっかりと暗記してしまいましょう(もちろん理解を伴った暗記ですよ)。
例題1
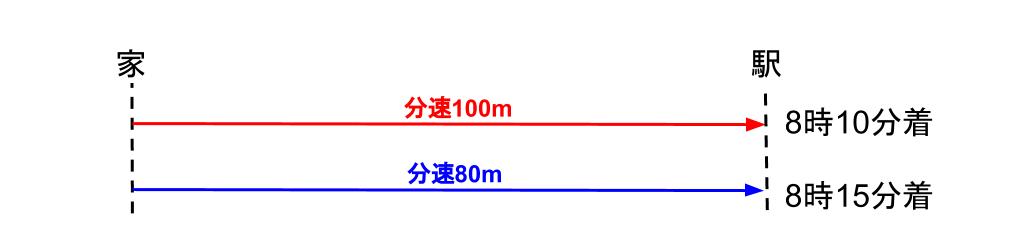
家から駅まで向かいます。分速100mで向かうと8時10分に、分速80mで向かうと8時15分に着きます。家から駅まで何mですか。また、家を出る時刻は何時何分ですか。
解説

いつも通りの図にするとこんなかな・・・

これはぜんぜん旅人算じゃない気がします。

うん。旅人算的状況じゃない、つまり時間の比が1:1ではないことがわかるのが第1歩だ。合格!!
線分図にこだわらないで、まずは比について式で考えてみてごらん。

はい、そうします。
速さはわかっている。
時間と距離のうち、どちらか片方がわかるはず・・・・
あっ。同じ距離です。どちらも、家から駅までの同じ距離。
距離の比が1:1だ。

ということは、かかった時間の比は、速さの比の逆の4:5だ!

もうカンペキです!!
残りあと少しがんばろー!

まだ使っていない情報は、8時10分と8時15分だから・・・
あれ?10分と15分は2:3??
あれ??

「出発時刻から8時10分までの経過時間」が④
「出発時刻から8時15分までの経過時間」が⑤
だよ。
時刻と時間はこんがらがらないでね。

出発時刻の④分後が、8時10分
出発時刻の⑤分後が、8時15分
つまり、到着までに①分多くかかると、5分遅く到着する。
つまり、①=5分だ!
だから、④=20分、⑤=25分だ。

あっ、ばっちりうまくいってます!!
家から駅までが2000mであることが、どちらの式からもでてきます。

正解!カンペキです。
あともう1つ。出発時刻は何時何分かな?

出発時刻の④=20分後が、8時10分
出発時刻の⑤=25分後が、8時15分
つまり、出発時刻は、7時50分です。

大正解!!
カンペキだよ!

異なる速さの2人が、同じ距離を進む問題。
速さの最重要パターンの1つです。
速さの異なる2人を比較して解くのだけれど、
太郎と次郎のように異なる2人の進み方を比較することもあれば、
太郎の「行き」と「帰り」を比較することもあるし、
太郎の「予定通りの速さで行く場合」と、「予定より急いでいく場合」を比較することもある。
様々なケースがあるからね。
そして大事なことなのだけれど、問題文で、
「距離の比が1:1だよ」とか、
「同じ距離だよ」のように強調されることはない。
だから、自分で読んで気が付かないといけないからね。距離が同じかどうか、常に意識しながら解いていくのですよ!!