1:差を集める(差集め算)
1:具体図で差を集める
差集め算という名称にこだわる必要はありません。
つるかめ算も、差を集めて解いていました。
同様の考え方、整理の仕方をするだけです。
例題1
何人かの生徒たちに折り紙を配ります。4枚ずつ配るための枚数と6枚ずつ配るための枚数の差が16枚のとき、生徒は何人いますか。
解説

今日はこんな問題だ。
つるかめ算で学習したことをこの問題でも発揮してちょーだいな。
さっそくやってみよう。

じゃあ、この問題もつるかめ算なんですか?

さあ、どうでしょう。

何算なのか教えてくださいよ。

いいから解いてちょーだい!

つるかめ算で学習したことは具体図だっだよ。
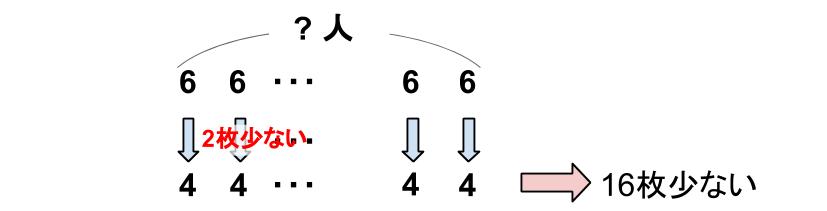

1人から2枚ずつ返してもらうと、全部で16枚になる。
つまり、16÷2=8
8人います。

お見事!具体図を上手に利用できたね。
具体図はいろいろなかきかたがあることも学んでおこう。
下図のように解くこともできるね。
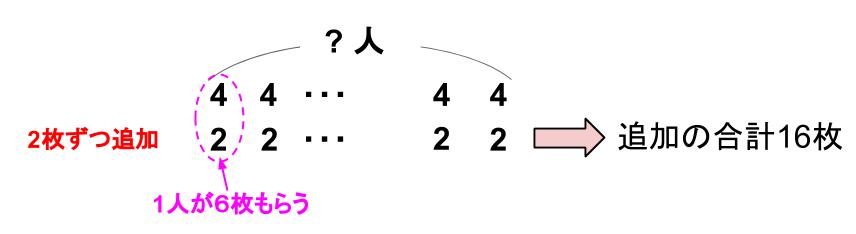

4枚ずつ配ったあとに、1人につき2枚ずつ追加する
という視点だよ。

ところで、どう?つるかめ算だった?

同じじゃないけど、そっくりでした。1つ1つの差を集めるところが。

その通り。「差を集める」という同じ考え方をして解いているんだね。
だから、同じ問題と言っても間違いじゃない。
しかし、そっくりだけど違う問題と言っても間違いじゃない。
結局、分類のやり方しだいで「同じ」とも「違う」とも言えるんだよ。

?

ワニとカメって違う動物だね。
でも、等しく「は虫類」で同じ仲間の動物だともいえる。
違うとも同じだともいえるわけ。
どこで区切るか次第。

そういうことか。

で、この問題はつるかめ算とは呼ばないんだ。
でもね、大事なことは「~算」という名前じゃない。
問題を読んで、それに合った整理の仕方をすれば、おのずと問題が解ける。
逆に、「~算」にあてはめるような考え方をしていると、
まったく問題が解けない固ーい頭になってしまう恐れがあるよ!
じゃあ類題で練習しよう!
参考
X+Y=P
aX+bY=Q
の連立方程式タイプをつるかめ算と呼びます。
また、6年生になれば、比を用いた別解もあります。
類題演習
リンゴを何個か買う予定でお店に行きました。リンゴより30円安いみかんを予定と同じ個数買うと、240円あまります。リンゴを何個買う予定でしたか。

あれ?えーっと、りんごもみかんも値段がわからないから・・・

例えば、リンゴが1個100円なら、
100 100 ・・・ 100
と書けたけど、いまはわからないから、
り り ・・・ り
と書いておくしかないよ。りんご1個が「り」だよ。
リンゴの絵をかくのはさすがに時間がかかるからね。


リンゴとミカンの値段の差は、1個で30円
240÷30=8
つまり、8個分の差が240円になる。
答えは8個!

うん、正解です!
