食塩水と面積図
1:食塩水と面積図

突然なんだけどね。食塩水は面積図と相性がいいんです。

はあ、そうなんですね。

今回は、食塩水において面積図という解法を使っていきます。
比を用いるので、比をまだ学習していない人は、比を学習した後にまた戻ってきてください。
さて、まずはきちんと理解するために、精密に食塩水の模式図をかきます。
いままではあまり精密にかいてなかったんだけどね。

まずは、濃さが20%の食塩水100gの図だ。
食塩水全体を10分割した図だよ。
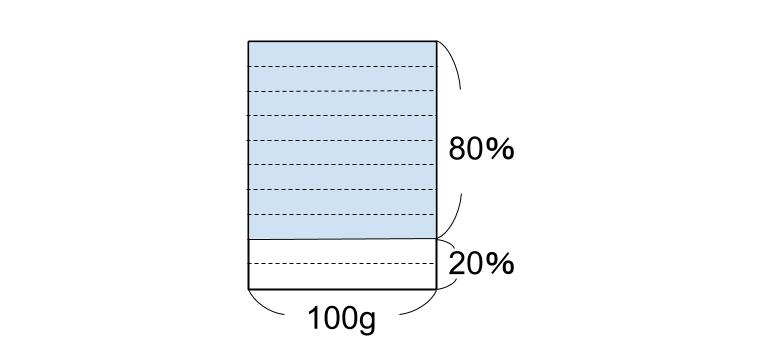

なるほど。水と食塩の割合を正確に表したんですね。

次に進むよ。
濃さが20%の食塩水100gと水100gをまぜるよ。
まぜたあとの食塩水は全体が200gで、とけている食塩は20gだから、濃さが10%になるのはわかるよね。

はい、わかります。

これは下の面積図のように表すことができるよね。
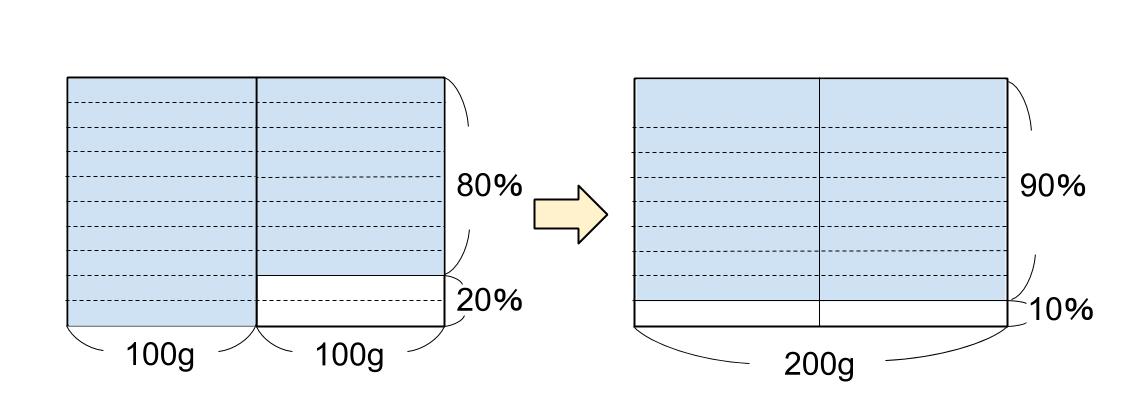

食塩が均一になりましたね。

食塩水にとけている食塩の量は、
(食塩の量)=(食塩水全体)×(濃さ)
で求められたよね。
この「食塩の量」は図において、「白い長方形の面積」で表現できているわけです。
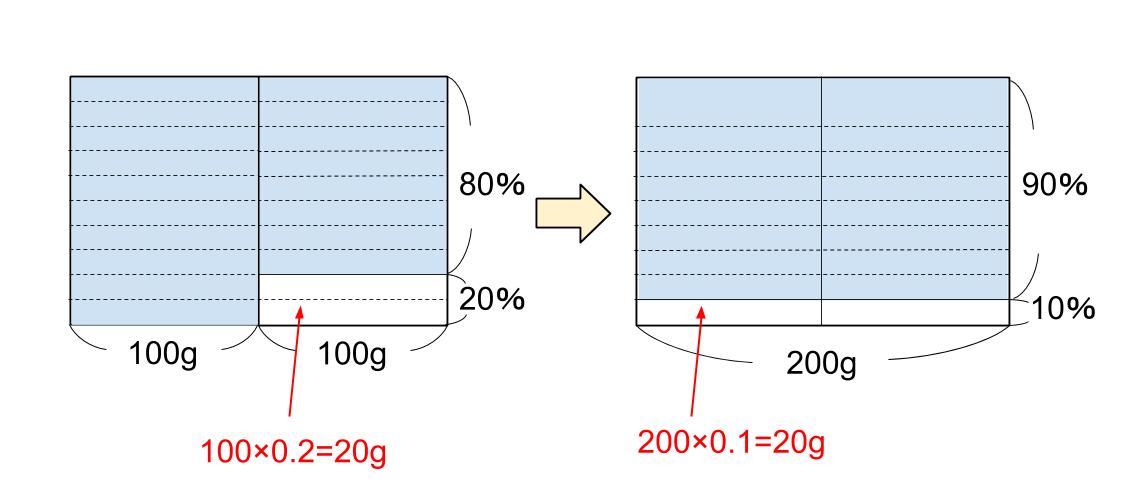

100g×20%=20g
200g×10%=20g
なるほど。食塩の量ってかけ算で求められるからな。
横が「食塩水の量」でたてが「濃さ」ならば、
横×たて=面積
「食塩水の量」×「濃さ」=「食塩の量」ですね。

そういうことです。
この面積図は、食塩水が変化して濃さが変わる問題を解くときに力を発揮します。
例えば上の例。
図をかく前に、計算で混合後の濃さを10%と求めたけれど、
面積図を使って下のように求めることもできる。
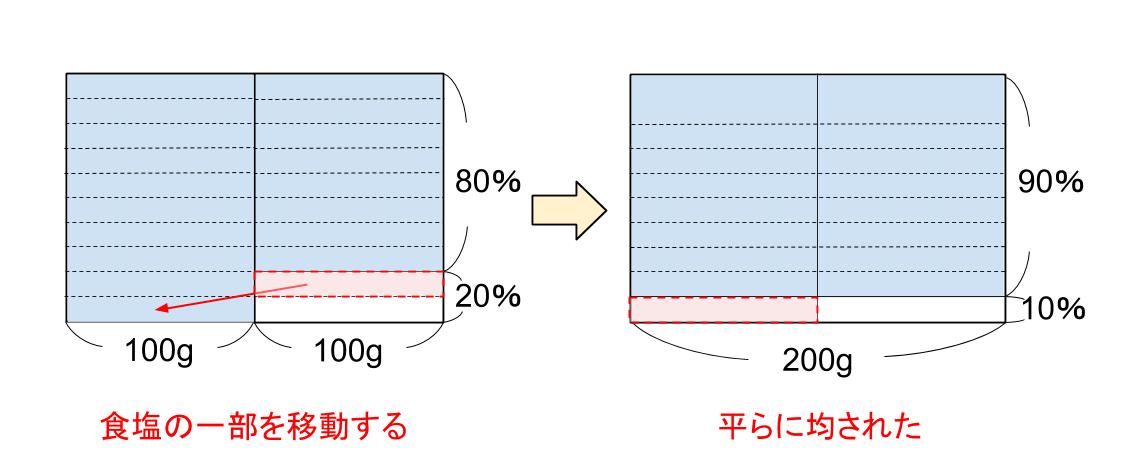

これは「平均」とまったく同じ考え方です。
食塩が濃い部分と薄い部分があって、まぜれば濃さが均一になる。
食塩水の混合は、平均と同じなのです。

なるほど。「均」って字も共通ですね。
平均と均一。
例題1
濃さが4%の食塩水100gと濃さが7%の食塩水200gをまぜると、濃さは何%になりますか。
解説

面積図なしで簡単に答えがでますよ。
全体が300gで、食塩が、4+14=18g
だから6%です!

うん正解です。
もちろん面積図なしでこの問題を解くことはできるね。
それに、学くんくらいサクッと簡単に計算で求める力をつけておくことも大事だ。
ただし、面積図なしでは解けない問題が今後出てくるんだ。
だから、この例題で面積図の練習をして理解を深めておきたいのです。
面積図の練習だよ。
まぜる前の図は下のようになる。
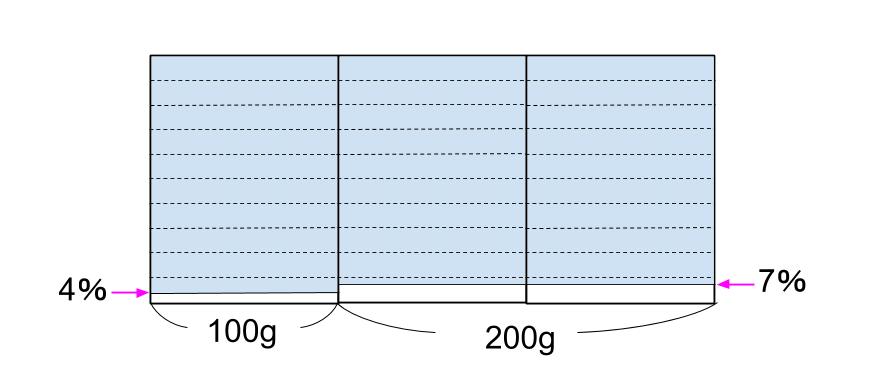

4%と7%を正確な比率で図示すると、図が小さすぎて見えにくいね。
だから、0%~10%のところをアップにした図で解くことにします。
図の上の方は無視をしましょう。
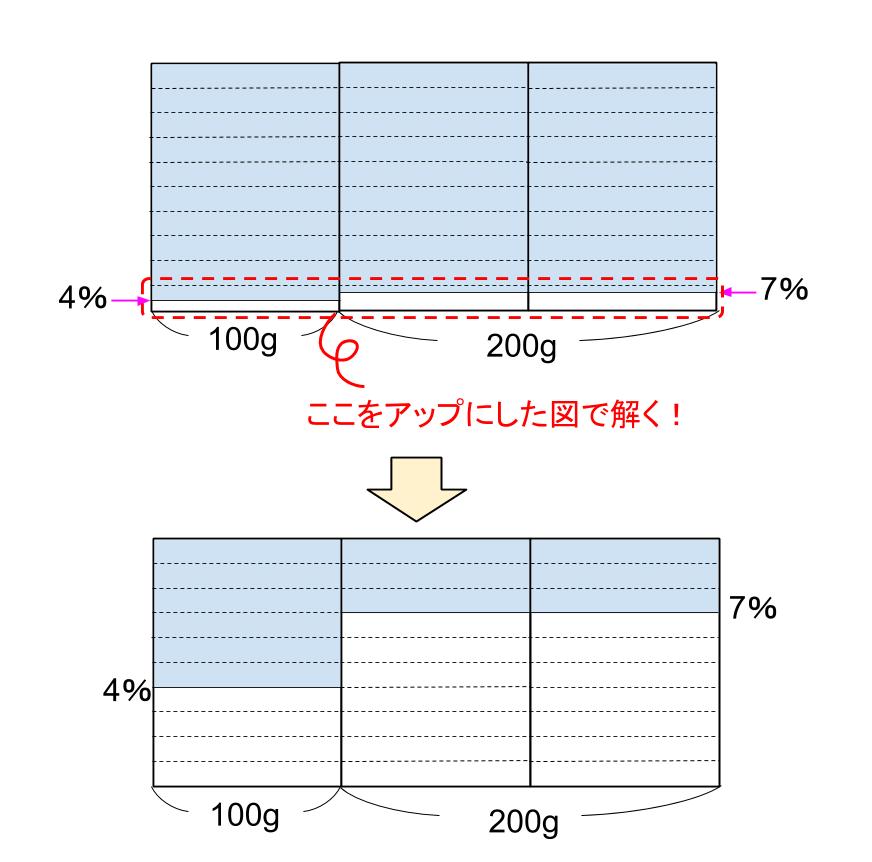

さて、
まぜると濃さが均一になるよね。

このデコボコの食塩を平らにすればいいんですね。
右上にある長方形を左下に移せば・・・
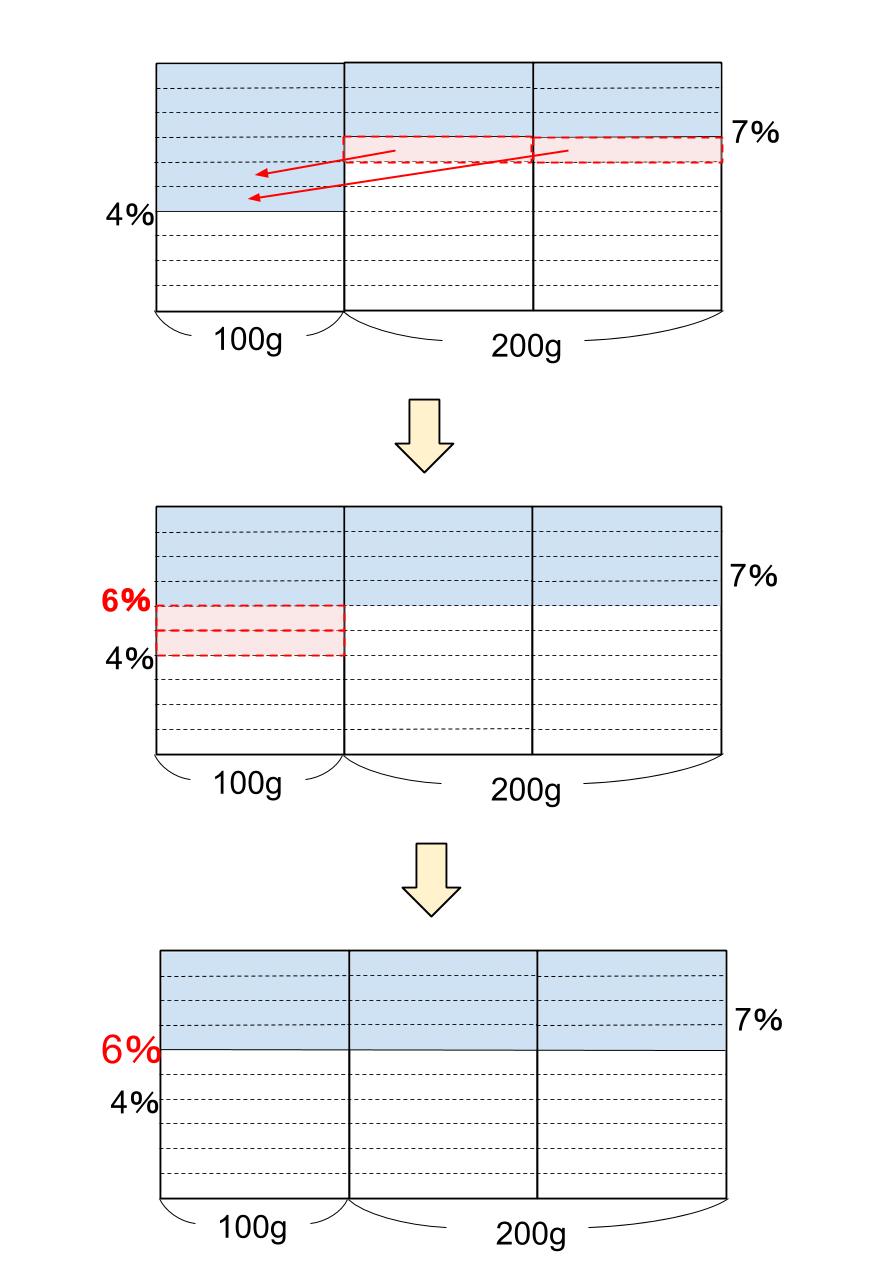

おお!
確かに図をいじくるだけで濃さ6%が求められました!
計算いらずです!

そういうことです。
ここで大事なことを確認しておくよ。
面積図で食塩を均一にするとき、図の上の方は使わなかったね。
つまり、「図の水の部分」はいらなかったよね。

あ!言われてみればそうですね。

今後は、食塩の上にある水の部分は省略した図をかくことにしよう。
食塩だけを注目した図で解いていくことができるからね。
